Algebra Formulas and Expression with Example

Algebra Formulas – What is Algebra?

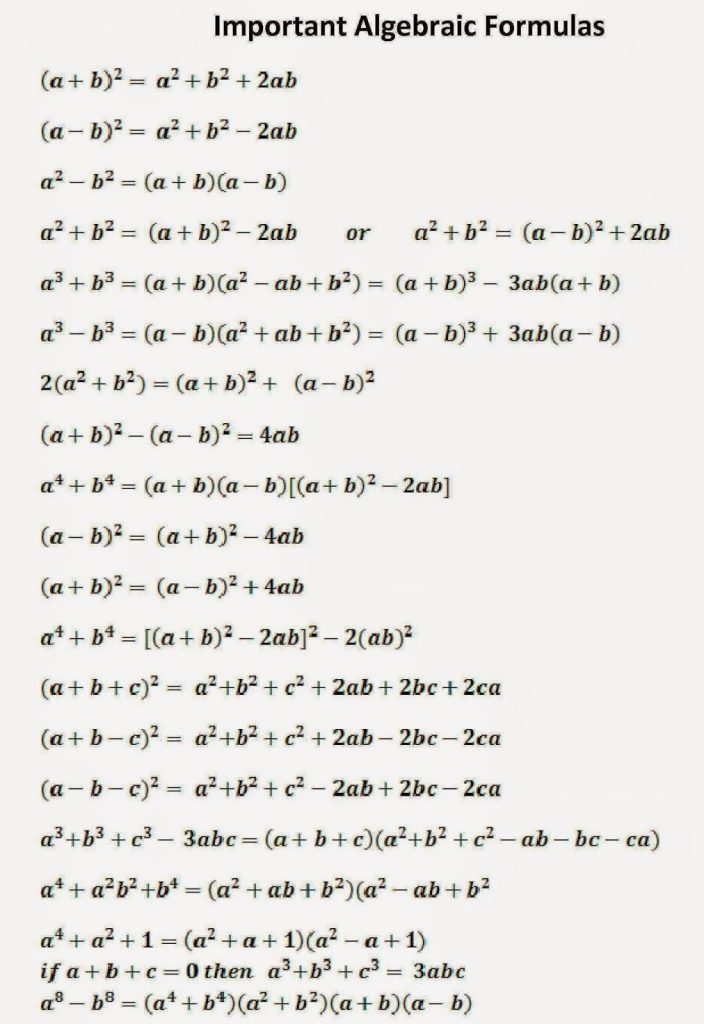
Algebra is basically a branch of mathematics which deals with symbols and the rules for manipulating with those symbols. Algebra allows you to substitute the values in order to solve the equations for the unknown quantities.

Algebra Formula

Algebra Formulas represents the relationship between the different variables. The variable can be taken as a, b, c, x, y or any other alphabet that represents a number unknown yet.

A list of Algebraic formulas

• a² – b² = (a – b)(a + b)
• (a+b)² = a² + 2ab + b²
• a² + b² = (a + b)² – 2ab
• (a – b)² = a² – 2ab + b²
• (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca
• (a – b – c)² = a² + b² + c² – 2ab + 2bc – 2ca
• (a + b)³ = a³ + 3a²b + 3ab² + b³ ; (a + b)³ = a³ + b³ + 3ab(a + b)
• (a – b)³ = a³ – 3a²b + 3ab² – b³
• a³ – b³ = (a – b)(a² + ab + b²)
• a³ + b³ = (a + b)(a² – ab + b²)
• (a + b)³ = a³ + 3a²b + 3ab² + b³
• (a – b)³ = a³ – 3a²b + 3ab² – b³
• (a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴)
• (a – b)⁴ = a⁴ – 4a³b + 6a²b² – 4ab³ + b⁴)
• a⁴ – b⁴ = (a – b)(a + b)(a² + b²)
• a⁵ – b⁵ = (a – b)(a⁴ + a³b + a²b² + ab³ + b⁴)
• If n is a natural number aⁿ – bⁿ = (a – b)(a^n-1 + a^n-2b+…+ b^n-2a + b^n-1)
• If n is even (n = 2k), aⁿ + bⁿ = (a + b)(a^n-1 – a^n-2b +…+ b^n-2a – b^n-1)
• If n is odd (n = 2k + 1), aⁿ + bⁿ = (a + b)(a^n-1 – a^n-2b +…- b^n-2a + b^n-1)
• (a + b + c + …)² = a² + b² + c² + … + 2(ab + ac + bc + ….)
• Laws of Exponents (a^m)(aⁿ) = a^m+n ; (ab)^m = a^mb^m ; (a^m)ⁿ = a^mn
• Fractional Exponents a⁰ = 1 ; aman=am−n ; am = 1a−m ; a−m = 1am

Roots of Quadratic Equation

• For a quadratic equation ax² + bx + c where a ≠ 0, the roots will be given by the equation as \[\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}\]
• Δ = b² − 4ac is called the discrimination
• For real and distinct roots, Δ > 0
• For real & coincident roots, Δ = 0
• For non-real roots, Δ < 0
• If α and β are the two roots of the equation ax² + bx + c then, α + β = (-b / a) and α × β = (c / a).
• If the roots of a quadratic equation are α and β, the equation will be (x − α)(x − β) = 0

Factorials

• n! = (1).(2).(3)…..(n − 1).n
• n! = n(n − 1)! = n(n − 1)(n − 2)! = ….
• 0! = 1
• \[\ (a + b)^{n} = a^{n}+na^{n-1}b+\frac{n(n-1)}{2!}a^{n-2}b^{2}+\frac{n(n-1)(n-2)}{3!}a^{n-3}b^{3}+….+b^{n}, where\;,n>1 \]

Algebra Problems with a Solution

Solved Examples of Algebra Formulas

Question 1: Find out the value of 5² – 3²
Solution:
Using the formula a² – b² = (a – b)(a + b)
where a = 5 and b = 3
(a – b)(a + b)
= (5 – 3)(5 + 3)
= 2 × 8
= 16

Question 2: 4³ × 4² = ?
Solution:
Using the exponential formula (a^m)(aⁿ) = a^m+n
where a = 4
4³ × 4²
= 4³⁺² = 4⁵ = 1024

Download Algebra Formula PDF

Click Here