The concepts of relations and functions are essential topics in Class 11 and 12. Below, you will find the function composition symbol, domain, and an example.
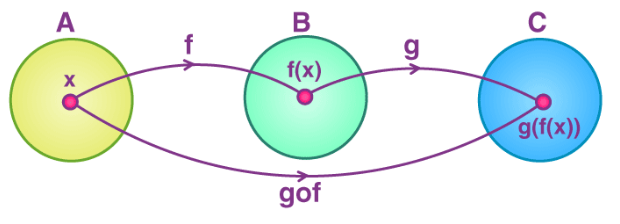
The composition of functions is a mathematical operation where the output of one function becomes the input of another function. If you have two functions, f(x) and g(x), their composition is written as:
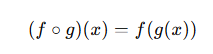
Topics Covered
Composition of Functions
How Composition of Functions Works?
- First, apply the function g to x, which gives g(x).
- Then, take that result and apply the function f to it, resulting in f(g(x)).
Examples of Composition of Functions
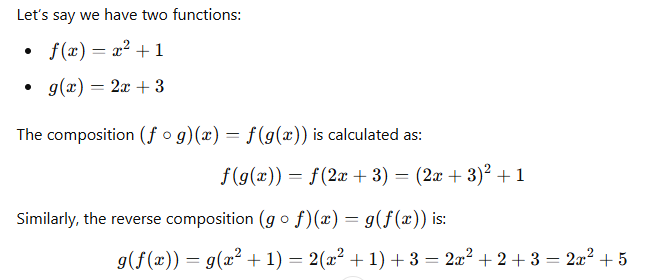
Key Properties of Composition of Functions
Non-Commutative: In general, f(g(x))≠g(f(x)).
Associativity: If there’s a third function h(x), then (f∘g)∘h=f∘(g∘h)
Identity Function: If I(x)=x then f∘I=f(x) and I∘f=f(x)
Important Questions – Composition of Functions
What is the composition of functions?
The composition of functions is the process of applying one function to the result of another function. If f(x)and g(x) are two functions, their composition is written as:(f∘g)(x)=f(g(x))
This means you first apply g(x), then apply f(x) to the result.
How do you compute the composition of two functions?
To compute (f∘g)(x):
- Find g(x).
- Substitute g(x)into f(x).
- Simplify if needed.
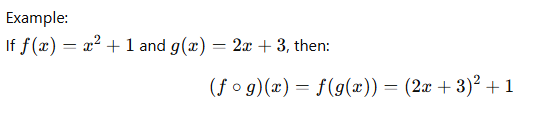
Is function composition commutative?
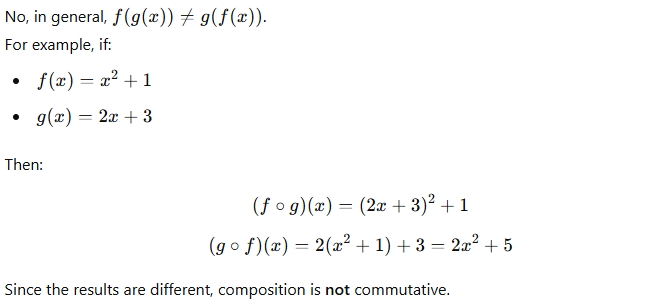
Can functions be composed infinitely?
Yes, but only if the output of one function remains within the domain of the next function. Some functions allow infinite composition, such as recursive functions in computer science.
Real-World Applications of Composition of Functions
Temperature Conversion
- Convert Celsius to Fahrenheit: F(C)=1.8C+32
- Convert Fahrenheit to Kelvin: K(F)=59(F−32)+273.15
- Composite function: K(C)=K(F(C))=59((1.8C+32)−32)+273.15=C+273.15
Finance (Compound Interest)
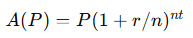
- P depends on initial deposits D(t), so we compose functions.
Physics (Motion)
- If s(t) is the position function and v(s) is velocity as a function of position, we can compute velocity as a function of time using composition.
Why is Function Composition Important?
- It helps in simplifying complex operations by breaking them into smaller functions.
- It is used in real-world applications, such as physics, economics, and computer science.
- It is a fundamental concept in calculus, especially in differentiation (chain rule) and integration.
Function composition is a powerful tool in mathematics that allows us to combine and manipulate functions effectively. It is widely used in real-world applications, making it an essential concept in various fields.
