Trigonometric identities are essential when working with expressions or equations that involve trigonometric functions. These identities hold true for every possible value of the variables on both sides of the equation. Geometrically, they pertain to certain trigonometric functions, such as sine, cosine, and tangent, of one or more angles.
The primary trigonometric functions include sine, cosine, and tangent, while the additional functions are cotangent, secant, and cosecant. Trigonometric identities incorporate all six of these functions. For related formulas, refer to Trigonometry Formulas.
Topics Covered
What are Trigonometric Identities?
Trigonometric identities are equalities involving trigonometric functions that hold true for all values of the variables in the equation.
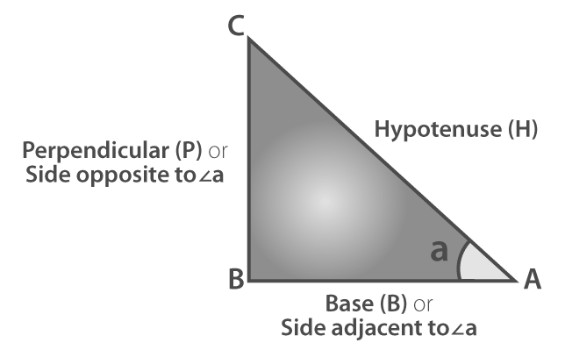
These identities are distinct and involve the side lengths and angles of a triangle. They are valid only for right-angled triangles.
Based on the six trigonometric ratios—sine, cosine, tangent, cosecant, secant, and cotangent—all trigonometric identities derive from these fundamental ratios. These ratios are defined using the sides of a right triangle: the adjacent side, opposite side, and hypotenuse.
List of Trigonometric Identities
1. Pythagorean Identities
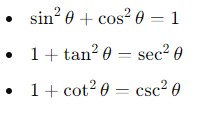
2. Reciprocal Identities
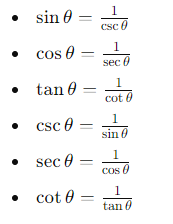
3. Quotient Identities
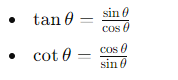
4. Co-Function Identities
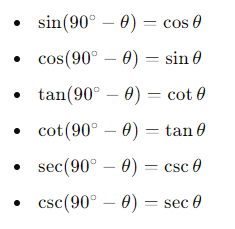
5. Even-Odd Identities
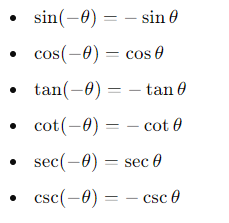
6. Sum and Difference Formulas
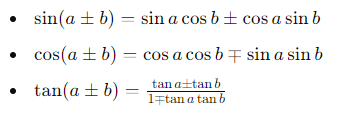
7. Double Angle Formulas
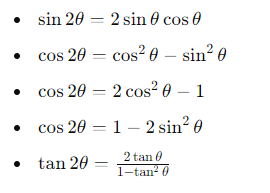
8. Half Angle Formulas
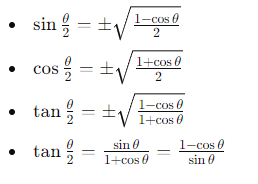
This comprehensive list of trigonometric identities provides essential tools for solving various mathematical problems involving trigonometric functions.
Trigonometric Identities Proofs
Pythagorean Identities
Proof of sin2𝜃+cos2𝜃=1sin2θ+cos2θ=1:

Proof of 1+tan2𝜃=sec2𝜃1+tan2θ=sec2θ:

Sum and Difference Formulas

Double Angle Formulas
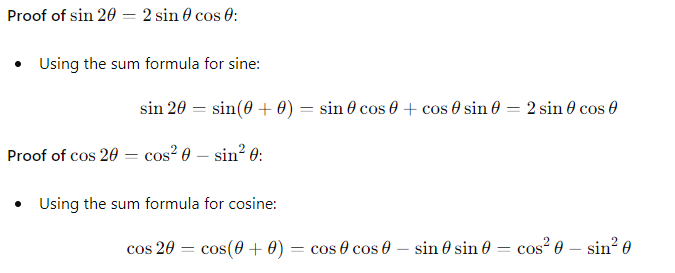
These proofs demonstrate the fundamental relationships between the trigonometric functions and provide the foundation for solving various trigonometric problems.
Frequently Asked Questions on Trigonometric Identities
1. What are trigonometric identities?
Trigonometric identities are equalities involving trigonometric functions that are true for all values of the variables for which the functions are defined. They are used to simplify expressions and solve equations involving trigonometric functions.
2. Why are trigonometric identities important?
Trigonometric identities are important because they provide relationships between the trigonometric functions that simplify the process of solving complex trigonometric equations. They are widely used in various fields, including engineering, physics, and mathematics.
3. What are the primary trigonometric identities?
The primary trigonometric identities include the Pythagorean identities, reciprocal identities, quotient identities, co-function identities, even-odd identities, sum and difference formulas, double angle formulas, and half-angle formulas.
4. How do you prove trigonometric identities?
To prove trigonometric identities, you typically start with one side of the identity and manipulate it using known identities and algebraic operations until it matches the other side. Proofs often involve substitution, factoring, and using fundamental trigonometric relationships.
5. How are trigonometric identities used in real life?
Trigonometric identities are used in various real-life applications, including engineering, physics, computer graphics, signal processing, and architecture. They help in analyzing wave patterns, designing structures, and solving problems related to periodic phenomena.
These FAQs cover the essential aspects of trigonometric identities and provide a solid foundation for understanding their importance and applications.
